Phase space disruption
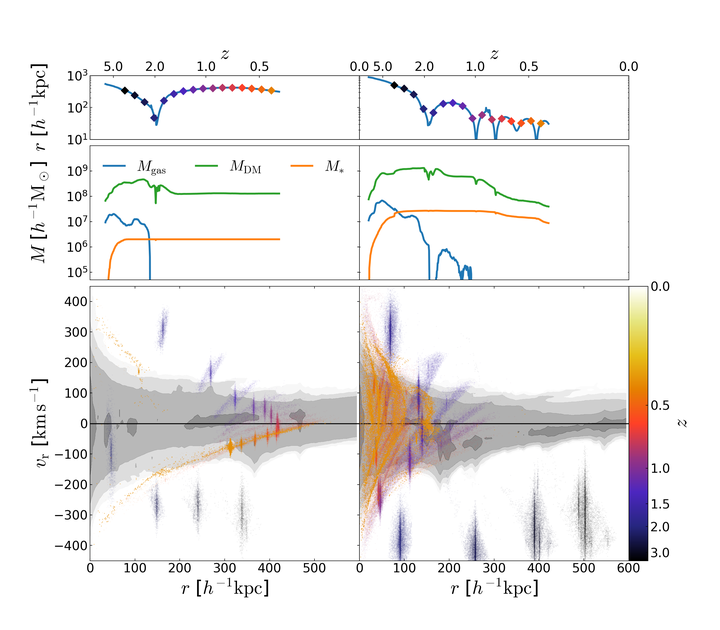
Caption: Galaxies grow over billions of years through a hierarchical process. Smaller objects merge and form larger ones, that then combine into even bigger ones. Most of these events involve galaxies with very unequal mass, and the fate of the smaller objects can be very different depending on their size and orbit. The movie shows the evolution of two such satellite galaxies orbiting similar (much bigger) hosts. The satellite in the left column has a mass 10 times smaller than the one on the right, and a 3 times larger impact parameter (i.e. its orbit starts more tangential). The top panels show the distance between each satellite galaxy and its host, as a function of redshift (a measure of time from the Big Bang, with today corresponding to redshift z=0). Since their orbit is a spiral, their distance from the host periodically changes. Additionally, they constantly loose energy because they move in a dense medium. This dynamical friction is more efficient for larger objects, and therefore the satellite on the right looses energy, and hence sinks at the center, more quickly. In addition, the pressure exherted on a satellite by its motion in a dense medium strips away its material. The mass reduction is stronger close to the host, where the density is higher. This effect can be seen in the central panels, that show the satellite mass as a function of redshift. The three curves refer to dark matter, gas, and stellar mass, and show that stripping is more efficient on the latter. The removed material becomes part of the host galaxy. To show this, in the bottom panels are shown all particles inside the satellite at the time it enters the hosts (z~2 for both columns), color-coded with redshift. The horizontal and vertical axes represent the position (distance) and velocity of the satellite galaxy with respect to the host. At regular intervals, marked by diamond symbols in the top panels, the particle position is impressed on the plot, to make evident their evolution. Finally, the gray shading in the background shows the distribution of all particles as density contours. Stripped particles end up overlapping with these contours, revealing they are well-mixed with the ambient medium. Despite being hosted by similar galaxies, and approaching them at similar times, the fate of the two satellites is very different. The one on the left survives until today, completes a single orbit and remains compact, thanks to its smaller mass and tangential orbit, that suppress the effects of dynamical friction and ambient pressure, respectively. The satellite on the left, however, is more affected by such effects because of its larger mass and more-radial trajectory. Its orbit decays quickly and brings it in region of higher density, enhancing the mass and energy loss. Consequently, the orbit is shrunk even more in a positive feedback loop that quickly destroys the satellite (when this happens, the lines in the top and middle panels stop).
Author: Enrico Garaldi
Affiliation: Max Planck Institute for Astrophysics
Original Image: link
# This script requires additional data file to run. Contact me if you are interested in having access to those
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as p
from matplotlib import gridspec
import numpy
import matplotlib.cm as cmaps
#--- SETTINGS
model1 = 1202
subID1 = 4324
model2 = 1236
subID2 = 3782
InitialSnap=80
FinalSnap=682
SnapStep=25
sim_type='all'
particles_type='all'
outfile='frame'
cmap_name = 'CMRmap'#'gist_ncar_r' #'Paired' #'Set1_r'
alpha = 0.1
dumpfile = 'dump'
#---SCRIPT
def customColorbar(fig, ax=None, cax=None, cmap='jet', norm=p.Normalize, vmin=0, vmax=1, orientation='vertical'):
sm = p.cm.ScalarMappable(cmap=p.get_cmap(cmap), norm=norm(vmin=vmin, vmax=vmax))
# fake up the array of the scalar mappable. Urgh...
sm._A = []
if ax is None and cax is None:
return fig.colorbar(sm, orientation=orientation)
elif ax is None:
return fig.colorbar(sm, cax=cax, orientation=orientation)
elif cax is None:
return fig.colorbar(sm, ax=ax, orientation=orientation)
else:
return fig.colorbar(sm, ax=ax, cax=cax, orientation=orientation)
#plotting stuff
fig = p.figure(figsize=(16,14))
gs1 = gridspec.GridSpec(7,29)
gs1.update(wspace=0.0, hspace=0.1)
ax1 = fig.add_subplot(gs1[3:7, 0:14])
ax2 = fig.add_subplot(gs1[3:7,14:28])
axt1 = fig.add_subplot(gs1[0 , 0:14])
axt2 = fig.add_subplot(gs1[0 ,14:28])
axm1 = fig.add_subplot(gs1[1:3, 0:14])
axm2 = fig.add_subplot(gs1[1:3,14:28])
axt1z=axt1.twiny()
axt2z=axt2.twiny()
axr = fig.add_subplot(gs1[3:7,28])
NUM_COLORS = (FinalSnap-InitialSnap) + 1
cm = p.get_cmap(cmap_name)
colors = [cm(1.*i/NUM_COLORS) for i in range(NUM_COLORS)]
boldSteps = list(range(InitialSnap,FinalSnap,SnapStep))
boldStepsColor = [colors[s - InitialSnap] for s in boldSteps]
#load snap-redshift correspondence
map_z = dict(dict(numpy.loadtxt('snap_redshift_map.txt',skiprows=1,usecols=[0,1])))
map_t = dict(dict(numpy.loadtxt('snap_redshift_map.txt',skiprows=1,usecols=[0,2])))
z_to_plot = [0, 0.5, 1, 2, 5]
t_to_plot = [13.720, 8.628, 5.903, 3.316, 1.186]
#contours data
data = numpy.load('dump_host_model1202.npz')
#remove Hubble flow
Hubble_flow = 100.0 * data['dist_v'] / 1e3 #kpc to Mpc
cc1202, xx1202, yy1202 = numpy.histogram2d(data['dist_v'], data['v_rad']+Hubble_flow, bins = 100)
#cc1202, xx1202, yy1202 = numpy.histogram2d(data['dist_v'], -data['v_rad'], bins = 100)
data = numpy.load('dump_host_model1236.npz')
#remove Hubble flow
Hubble_flow = 100.0 * data['dist_v'] / 1e3 #kpc to Mpc
cc1236, xx1236, yy1236 = numpy.histogram2d(data['dist_v'], data['v_rad']+Hubble_flow, bins = 100)
#cc1236, xx1236, yy1236 = numpy.histogram2d(data['dist_v'], -data['v_rad'], bins = 100)
frame_counter = 0
def plot_snap(this_snap, bs_alpha):
print('FRAME ', this_snap)
for i,(model,subID) in enumerate(zip([model1,model2],[subID1,subID2])):
if i==0:
axt = axt1
axtz=axt1z
axm = axm1
ax = ax1
cc = cc1202
xx = xx1202
yy = yy1202
elif i==1:
axt = axt2
axtz=axt2z
axm = axm2
ax = ax2
cc = cc1236
xx = xx1236
yy = yy1236
ax.contourf(xx[:-1], yy[:-1], numpy.log10(cc.T), 5, vmin=1, cmap=p.cm.Greys, alpha = 0.5)
#load catalog
snaps,sh_ID,sh_cx,sh_cy,sh_cz,sh_vx,sh_vy,sh_vz,sh_npart,sh_Mvir,sh_Rvir,sh_Rmax,sh_r2,sh_Vmax,sh_Vesc,sh_sigmaV,\
sh_SpinB,sh_SpinP,sh_b, sh_c,sh_Cparam,sh_Mgas,sh_Mstar,sh_dist,h_ID,h_cx,h_cy,h_cz,h_vx,h_vy,h_vz,h_npart,h_Mvir,\
h_Rvir,h_Rmax,h_r2,h_Vmax,h_Vesc,h_sigmaV,h_SpinB,h_SpinP,h_b,h_c,h_Cparam,h_Mgas,h_Mstar \
= numpy.loadtxt('model%i_subhalo%i.dat'%(model, subID),unpack=True)
#first, plot bold steps until now
for k,bstep in enumerate(boldSteps):
if bstep < this_snap:
data = numpy.load(dumpfile+'_model%i_snap%i.npz'%(model, bstep))
dist = data['dist_v']
v_rad = data['v_rad']
ax.plot(dist,v_rad, '.', linewidth=0, markersize=0.5, alpha=bs_alpha, color=boldStepsColor[k])
#history in a top panel
z = numpy.array([map_z[s] for s in snaps])
t = numpy.array([map_t[s] for s in snaps]) #time in Gyr
w=(snaps <= this_snap)
axt.plot(t[w],numpy.sqrt((sh_cx[w]-h_cx[w])**2 + (sh_cy[w]-h_cy[w])**2 + (sh_cz[w]-h_cz[w])**2),'C0-', linewidth=3)
#masses in middle panel
axm.plot(t[w],sh_Mgas[w], 'C0-', label=r'$M_{\rm{gas}}$', linewidth=3)
axm.plot(t[w],sh_Mvir[w], 'C2-', label=r'$M_{\rm{DM}}$' , linewidth=3)
axm.plot(t[w],sh_Mstar[w],'C1-', label=r'$M_{\rm{*}}$' , linewidth=3)
if this_snap > FinalSnap:
data = numpy.load(dumpfile+'_model%i_snap%i.npz'%(model, FinalSnap))
dist = data['dist_v']
v_rad = data['v_rad']
ax.plot(dist,v_rad, '.', linewidth=0, markersize=0.5, color=colors[FinalSnap-InitialSnap])
else:
data = numpy.load(dumpfile+'_model%i_snap%i.npz'%(model, this_snap))
dist = data['dist_v']
v_rad = data['v_rad']
ax.plot(dist,v_rad, '.', linewidth=0, markersize=0.5, color=colors[this_snap-InitialSnap])
for k,bstep in enumerate(boldSteps):
if bstep < this_snap:
if bstep in snaps:
axt.plot([map_t[bstep]], [sh_dist[snaps==bstep]], 'D', linewidth=1, markersize=8, color=boldStepsColor[k])
else:
axt.plot([map_t[bstep]], [12], 'D', linewidth=1, markersize=8, color=boldStepsColor[k])
#colorbar
cb = customColorbar(fig, cax=axr, cmap=cmap_name, vmin=InitialSnap, vmax=FinalSnap, orientation='vertical')
#cb.ax.xaxis.set_ticks_position('top')
#ticks = numpy.linspace(InitialSnap,FinalSnap,5,endpoint=True)
ticks = [98, 155, 205, 283, 421, FinalSnap] #z= 3,2,1.5, 1, 0.5, 0.0
cb.set_ticks(ticks)
cb.set_ticklabels(["3.0", "2.0", "1.5", "1.0", "0.5", "0.0"])
cb.set_label('$z$', fontsize=30)
#cosmetics
axt.set_xticks([])
axt.set_xticklabels([])
axt.set_xlim([0,13.8])
axt.set_ylim([10,1000])
axt.set_yscale('log')
if i==0:
axt.set_ylabel(r'$r$ [$h^{-1} \rm{kpc}$]', fontsize=30)
axt.set_yticks([10,100,1000])
elif i==1:
axt.set_yticks([])
axtz.set_xticks(t_to_plot)
axtz.set_xticklabels(["%.1f"%(zz) for zz in z_to_plot])
axtz.set_xlabel('$z$', fontsize=30)
axm.set_xticks([])
axm.set_xlim([0,13.8])
axm.set_ylim([5e4,9.9e9])
axm.set_yscale('symlog')
if i==0:
axm.set_ylabel(r'$M$ [$h^{-1} \rm{M_\odot}$]',fontsize=30)
axm.legend(loc='upper left', fontsize=24, ncol=3, handlelength=1.4)
elif i==1:
axm.set_yticks([])
#align labels
axt.yaxis.set_label_coords(-0.15, 0.5)
axm.yaxis.set_label_coords(-0.15, 0.5)
ax .yaxis.set_label_coords(-0.15, 0.5)
ax.hlines(0,0,1000,color='k')
ax.set_xlim([0,600])
ax.set_ylim([-450,450])
ax.set_xlabel(r'$r$ [$h^{-1} \rm kpc$]',fontsize=30)
if i==0:
ax.set_ylabel(r'$v_{\rm r}$ [$\rm km \, s^{-1}$]',fontsize=30)
ax.set_xticks([0, 100, 200, 300, 400, 500])
elif i==1:
ax.set_yticks([])
ax.set_xticks([0, 100, 200, 300, 400, 500, 600])
ax.tick_params(axis='both', labelsize=20)
axt.tick_params(axis='both', labelsize=20)
axtz.tick_params(axis='both', labelsize=20)
axm.tick_params(axis='both', labelsize=20)
cb.ax.tick_params(axis='both', labelsize=20)
#cleanup
fig.savefig(outfile+'_%i.png'%(this_snap-InitialSnap), bbox='tight')
ax1 .cla()
ax2 .cla()
axm1.cla()
axm2.cla()
axt1.cla()
axt2.cla()
for this_snap in range(InitialSnap, FinalSnap):
plot_snap(this_snap, alpha)
#now ramp up the alpha
alpha_ramp = numpy.concatenate([ alpha*numpy.ones(25), numpy.linspace(alpha,1,50), numpy.ones(75) ])
for l,a in enumerate(alpha_ramp):
plot_snap(FinalSnap+l, a)
Press the tag below to see more examples